The case for abstraction in biology

In clinical medicine, we must routinely make high-stakes decisions about complex systems with incomplete information. For example, consider a patient in shock, a potentially deadly condition in which bodily organs do not receive sufficient oxygen to perform their functions. Patients often present with dangerously low blood pressures. The treatment of shock depends on the underlying cause, which can range from poor heart function to uncontrolled infection. These patients are often some of the sickest in the hospital, but also require swift treatment (in septic shock, mortality increases by ~4% for every hour treatment is delayed [1]).

How can we make rapid decisions in this context? Knowing the exact state of every component of the system is impossible. Furthermore, it is unlikely to be useful, as the same underlying pathology can manifest differently depending on the patient. Instead, clinical decision-making makes use of simple abstractions that enable inference of the status of the system based on a limited number of parameters. Shock is a canonical example of this type of abstraction. A framework for identifying the etiology of shock is based on an understanding that shock usually manifests with low blood pressure. Mean arterial blood pressure (MAP) is proportional to the product of cardiac output and systemic vascular resistance (MAP=COxSVR). This simple equation informs an approach to analyzing shock and determining the appropriate treatment. We can measure these parameters using hemodynamic instruments and physical exam maneuvers. For example, a patient with cardiogenic shock, due to a problem with the heart, would have a low CO (which could be seen on a heart ultrasound or via hemodynamic measurements) and increased SVR (which could be calculated from hemodynamic measurements and inferred from cool-feeling extremities on exam). This might be treated by removing fluids that back up due to poor forward heart flow and using medications or devices to augment heart function. On the other hand, a patient with septic shock from infection would have warm extremities (low SVR) and preserved or increased cardiac output, and could be treated with antibiotics, additional fluids, and medications to increase the blood pressure. These simple abstractions do not fully describe the system but are “good enough” heuristics to enable mental manipulation and decision making. Thus, in the clinic, integrated thinking coupled with simple, quantitative descriptions allow interpretation of complex situations with limited information.

In contrast, in the laboratory, modern biological research has gradually moved away from integrated, quantitative theories of system behavior to instead emphasize increasingly detailed understanding of individual components of each system. As our ability to measure has improved, the impulse to integrate has waned. We can measure the identity and quantity of DNA, RNA, and protein in individual cells. We can watch proteins move at super-resolution in live cells and animals. We can even create precise genetic edits in primary cells. However, we have fewer abstracted principles that can make predictions about how a system might respond to different perturbations. This is especially stark in pathologies that affect not just individual cells, but tissue-level states, such as fibrosis, cancer, and neurodegeneration. Which are the homeostatic variables, signals, and/or cell types whose regulation controls irreversible branch points into healthy vs diseased tissue? What is the threshold concentration of a cytokine or antigen needed to alter an immune response? What are the appropriate ratios of different cell types or metabolites to maintain tissue homeostasis? What is the equivalent of MAP=COxSVR which describes whether a tissue will undergo healthy regeneration and repair vs pathologic fibrosis? Such abstractions have, for the most part, not been the goal of modern biological investigation.

This was not always the case. The early years of the molecular biology revolution were marked by the crossover of physicists to biology who brought with them a strong respect for the power of theory and models. This approach enabled many landmark discoveries. In some cases, mathematical models predicted the discovery of unknown biological entities. For example, the Hodgkin-Huxley model of the action potential in the 1950s predicted the existence of voltage-gated ion channels, which were not cloned until the 1980s [2]. Even further back in history, Mendel’s mathematical descriptions of inheritance patterns predated the discovery of genes as a physical entity by over a century. In other cases, abstraction enabled inference of mechanism. The Luria-Delbruck experiment showed that mutations and genetic diversity existed prior to, and were not induced by, selective pressure. They did so by comparing the observed distribution of bacterial colonies resistant to phage to the Poisson distribution that would be predicted under a model in which resistance was induced by selective pressures. In this case, inference of mechanism relied on a mathematical abstraction of observed phenomena [3] [4]. In a time when scientists had limited understanding of biological systems, abstraction and theory pointed the field in the most productive directions.

What has driven this shift away from abstraction? One factor has been the souring on the value of theory in the face of biological complexity [4] [5]. Abstraction at a higher level may reveal general principles but fail to generalize to variation in experimental conditions. For example, a model of receptor-binding conditions in one context may fall apart when salt concentrations are altered. In more dramatic instances, grand proposals for universal generalization which have failed to meet their hype have further fueled skepticism of the ability of models to predict the idiosyncrasies of biological systems [6] [7] [8]. Some changes also reflect differences in training. For example, theorists who rely on mathematics may have a harder time communicating with experimentalists. Furthermore, although many biologists may make implicit assumptions about the systems that they study, those who explicitly write these down as formal models may open themselves up to criticism based on the specifics of their modeling decisions. Finally, increasing specialization and siloing has decreased the opportunities for integrated thinking about biological systems. That models cannot perfectly capture biology at every level has led to skepticism of their utility at any level.

Figure 1 - Birds flying in formation (from WikiMedia): a classic example of a complex system in which the behavior of the system depends on interactions between system components. In this case, bird formations can be described by simple rules governing interactions between each bird and its closest neighbors in the flock.

This challenge is not unique to biology. The entire field of complex systems aims to develop theories for discovering the simple sets of rules which govern interactions between interconnected agents to give rise to system-level emergent properties. Classic examples are explanations of bird flocking or insect social behavior (Figure 1). In these cases, understanding the behavior of individual components (e.g. a single insect or a single bird) is insufficient to describe the behavior of the system, and instead depends on deriving the rules that control the interactions between these components. For example, in the case of birds, early simulation work showed that “flocking” could be achieved through simple algorithms based on three principles of how birds in a flock interact with their neighbors [9]. More recently, this has been refined through data-driven models from high-speed camera measurements, where each bird’s behavior can be described in relation to its closest neighbors in the flock [10] [11] [12]. These examples demonstrate the value of a priori emphasis on simple rules that underlie interactions between system components over exhaustively detailed descriptions of individual system members. This has many parallels in molecular and cellular biology, where tissues can be conceptualized as complex systems composed of hierarchical interactions between cells that contribute to and depend on different tissue functions. Thus, making the abstraction the goal rather than an afterthought can discover principles that would be missed by detailed descriptions of individual system components alone.

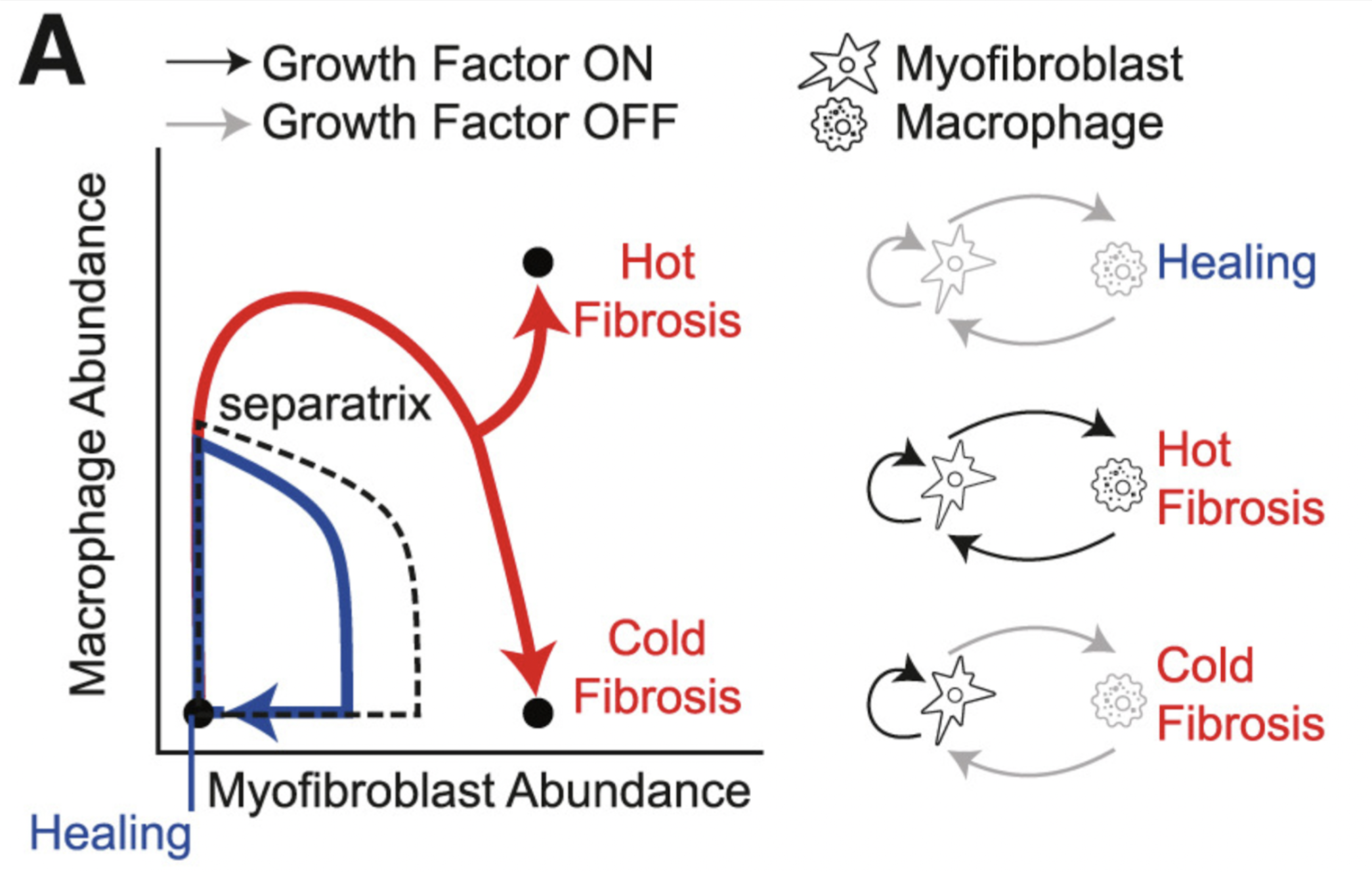Figure 2 - Reproduced from [14]. The authors use a combination of mathematical modeling and experiments to derive the thresholds at which hearts undergo different forms of fibrosis, depending on relative ratios of the abundance of macrophages and myofibroblasts. This is an interesting example of deriving quantitative principles that describe transitions in the state of a biological system.

There is still some hope. Experimental biology is unique because we can measure, abstract, and manipulate systems. Recent examples have highlighted the power of abstraction in deriving principles of biological organization. For example, some have used in vitro co-culture models where cell and growth factor concentrations can be tightly controlled to derive a simple, quantitative circuit that explains population sizes and cell-cell interactions between macrophages and fibroblasts [13]. Furthermore, the authors used mathematical models to make predictions of different hypotheses of system control that could then be tested experimentally. Similar circuit modeling approaches have been applied to understand more complex in vivo phenotypes, such as fibrosis resulting from heart pressure overload versus myocardial infarction. Interestingly, in that context, the authors use both computation and experiments to identify unstable points that control transition of the tissue to fibrosis versus repair [14] (Figure 2). More recently, some have even used synthetic biology to engineer “synthetic organizer” cells that can secrete morphogens to influence tissue organization, opening the door for experimental testing of such quantitative predictions [15]. Such studies are increasingly combining both theory and experiment to derive testable and quantitative principles of biological organization. Importantly, they are beginning to uncover the principles of interactions between system components.

What would an emphasis on abstraction enable in biology? We can only discover the simple rules that generate complex biological phenomena if we are intentional in searching for them. Including abstraction as part of the goal of biological research will enable us to search for such principles. Beyond understanding the processes that generate the beauty and complexity of biology, greater abstraction will open the door to manipulation of biological systems by identifying the key nodes that control their behavior. Much as we can determine the appropriate type of shock, and the corresponding ideal treatment based on physiological parameters, abstractions of biological systems could inform manipulations which could shift tissue states, as in the fibrosis example above. Finally, abstraction can inform future experimental directions. As in the examples from classic molecular biology, mental manipulation through abstraction will enable inference of predicted, but un-discovered mechanisms. Especially in the age of AI, the places where abstractions or models are most uncertain are likely to be the areas in which investment of further experimental resources will be most productive.

In his famous lecture, Freeman Dyson contrasts two types of researchers: birds, which “fly high in the air and survey broad vistas…[and] delight in concepts that unify our thinking,” and frogs, which “live in the mud below and see only the flowers that grow nearby…[and] delight in the details of…problems one at a time.” [16] Progress in science requires both “frogs” to reveal the intricate details of beautiful systems and “birds” to synthesize these observations into generalizable principles. In the clinical sphere, where we are forced to make decisions with coarse clinical measurements, abstraction enables us to reason with limited data. In biology, we have the luxury of understanding complexity at a fine-grained level. However, this should not prohibit synthesis of simple, unifying, and predictive rules. Even if imperfect, such abstractions will provide a compass by which to drive biological discovery forward.

References